Camera Animation, Part II

Camera Animation with a cubic spline:





So last time I lied a little bit about our camera path. I showed this picture:


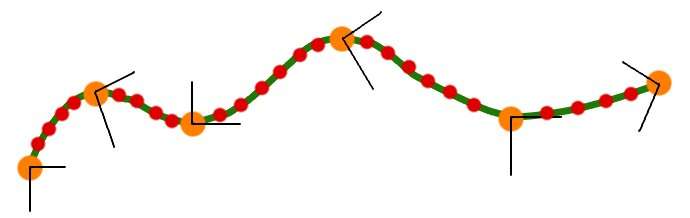
to describe the path that we wanted. But with linear interpolation, what we really ended up with was something like:


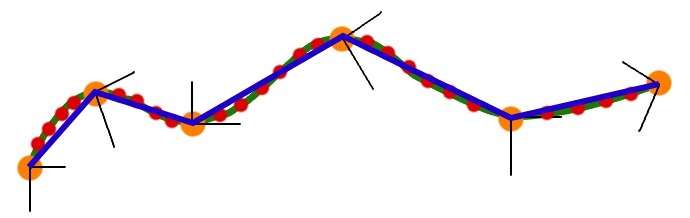
But today, I'll introduce cubic spline interpolation, and this will produce a truly smooth curve. Most of the code is the same, the only thing that has changed is that I have added a cubic option to the build function and have changed the animation to be reliant on time.

Building the natural cubic spline is more math intensive than with linear interpolation, so to start out here's a few links on cubic splines:

• http://mathworld.wolfram.com/CubicSpline.html
• http://www.physics.utah.edu/~detar/phycs6720/handouts/cubic_spline/cubic_spline/node1.html
• http://www.cse.unsw.edu.au/~lambert/splines/
• An Introduction to Splines for Use in Computer Graphics and Geometric Modelling
  

//a point on a cubic spline is affected by every other point
//so we need to build the cubic equations for each control point
//by looking at the entire curve. This is what calculateCubicSpline does
Vector3[] looks = new Vector3[mKeyFrames.Count];
Vector3[] positions = new Vector3[mKeyFrames.Count];
Vector3[] ups = new Vector3[mKeyFrames.Count];

for (int i = 0; i < mKeyFrames.Count; i++)
{
    looks[i] = mKeyFrames[i].Look;
    positions[i] = mKeyFrames[i].Position;
    ups[i] = mKeyFrames[i].Up;
}

Cubic[] pos_cubic = calculateCubicSpline(mKeyFrames.Count - 1, positions);
Cubic[] look_cubic = calculateCubicSpline(mKeyFrames.Count - 1, looks);
Cubic[] up_cubic = calculateCubicSpline(mKeyFrames.Count - 1, ups);

for (int i = 0; i < mKeyFrames.Count - 1; i++)
{
    for (int j = 0; j < mPathSteps; j++)
    {
        float k = (float)j / (float)(mPathSteps - 1);

        Vector3 center = pos_cubic[i].GetPointOnSpline(k);
        Vector3 up = up_cubic[i].GetPointOnSpline(k);
        Vector3 look = look_cubic[i].GetPointOnSpline(k);

        Vector3 r = Vector3.Cross(up, look);
        Vector3 u = Vector3.Cross(look, r * -1f);

        Camera cam = new Camera();
        cam.SetLens(mFOV, mAspect, mNearZ, mFarZ);
        cam.Place(center, look, u);

        cam.BuildView();

        mCameraPath.Add(cam);
    }
}

So the first thing we do is build the cubic polynomials for each control point. And because each point controls the shape of the spline, we have to consider each point when building the polynomials. In this way, it is very different from linear interpolation in that we have to know information about the whole curve to perform a cubic interpolation rather than just the current and next control point as with linear interpolation. You might be thinking that "well Vector3 already contains a SmoothStep function that performs cubic interpolation". And you're right it does, but just interpolating the two points without knowledge of the whole curve still produces segmented(i.e. not smooth) animation. Once we have the polynomials for each control point, we can perform a cubic interpolation by just looking at the current and next control point, in the same fashion that we did with linear interpolation.

This is what the calculateCubicSpline function does, it builds polynomials for each control point, successively building off of the last control point's polynomial. Let's look at it:

Vector3[] gamma = new Vector3[n + 1];
Vector3[] delta = new Vector3[n + 1];
Vector3[] D = new Vector3[n + 1];
int i;
/* We need to solve the equation
 * taken from: http://mathworld.wolfram.com/CubicSpline.html
   [2 1       ] [D[0]]   [3(v[1] - v[0])  ]
   : 1 4 1    : :D[1]:   :3(v[2] - v[0])  :
   :  1 4 1   : :  . : = :       .        :
   :  .....   : :  . :   :       .        :
   :     1 4 1: :  . :   :3(v[n] - v[n-2]):
   [       1 2] [D[n]]   [3(v[n] - v[n-1])]

   by converting the matrix to upper triangular.
   The D[i] are the derivatives at the control points.
 */

//this builds the coefficients of the left matrix
gamma[0] = Vector3.Zero;
gamma[0].X = 1.0f / 2.0f;
gamma[0].Y = 1.0f / 2.0f;
gamma[0].Z = 1.0f / 2.0f;
for (i = 1; i < n; i++)
{
    gamma[i] = Vector3.One / ((4 * Vector3.One) - gamma[i - 1]);
}
gamma[n] = Vector3.One / ((2 * Vector3.One) - gamma[n - 1]);

delta[0] = 3 * (v[1] - v[0]) * gamma[0];
for (i = 1; i < n; i++)
{
    delta[i] = (3 * (v[i + 1] - v[i - 1]) - delta[i - 1]) * gamma[i];
}
delta[n] = (3 * (v[n] - v[n - 1]) - delta[n - 1]) * gamma[n];

D[n] = delta[n];
for (i = n - 1; i >= 0; i--)
{
    D[i] = delta[i] - gamma[i] * D[i + 1];
}

// now compute the coefficients of the cubics
Cubic[] C = new Cubic[n];
for (i = 0; i < n; i++)
{
    C[i] = new Cubic(v[i], D[i], 3 * (v[i + 1] - v[i]) - 2 * D[i] - D[i + 1],
             2 * (v[i] - v[i + 1]) + D[i] + D[i + 1]);
}
return C;

Once we find the cubic equation for each control point (key frame), we can use GetPointOnSpline() uses the cubic equation to calculate the intermediate point along the cubic spline.

public Vector3 GetPointOnSpline(float s)
{
    return (((d * s) + c) * s + b) * s + a;
}

And that's it. Now we have a smooth animation of our camera. There are many more ways to calculate the curve, including: hermite curves, b-splines, bezier curves, catmull-rom splines, NURBS(Nonuniform Rational B-Splines) and others. Microsoft also has a sample on creating a camera path that appears to be using hermite curves. But they hide all the details from you, and it's just more interesting to know the math behind it isn't it ;) ?